
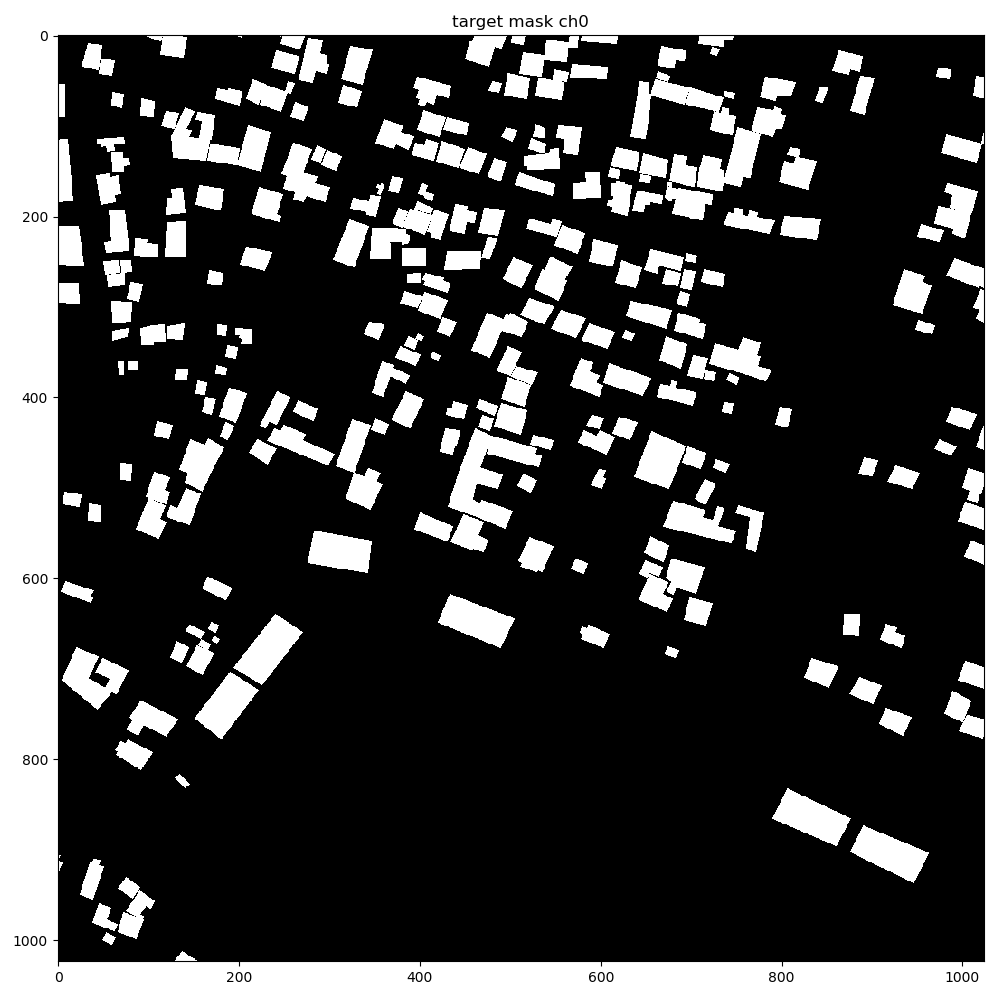
Xe = softmax_cross_entropy(labels, logits) Return -torch.sum(labels * normalized_logits) Normalized_logits = scaled_logits - torch.logsumexp(scaled_logits, dim) Scaled_logits = logits - torch.max(logits) We can rewrite this by expanding the softmax and doing some simplifications:ĭef softmax_cross_entropy(labels, logits, dim=-1): Note that in this implementation as the softmax output approaches zero, the log's output approaches infinity which causes instability in our computation. Xe = unstable_softmax_cross_entropy(labels, logits) So a naive implementation of the cross entropy would look like this:ĭef unstable_softmax_cross_entropy(labels, logits): Recall that cross entropy for a categorical distribution can be simply defined as `xe(p, q) = -Σ p_i log(q_i)`. We then define our loss function to be the cross entropy between our predictions and the labels.

We use the softmax function to produce probabilities from our logits. Consider we have a classification problem. Print(softmax(torch.tensor()).numpy()) # prints This way the domain of the exponential function would be limited to ``, and consequently its range would be `` which is desirable:Įxp = torch.exp(logits - torch.reduce_max(logits)) We choose this constant to be the maximum of logits. Therefore we can subtract any constant from the logits and the result would remain the same. It's easy to see that `exp(x - c) Σ exp(x - c) = exp(x) / Σ exp(x)`. The largest valid logit for our naive softmax implementation is `ln(3.40282e+38) = 88.7`, anything beyond that leads to a nan outcome.īut how can we make this more stable? The solution is rather simple. Note that computing the exponential of logits for relatively small numbers results to gigantic results that are out of float32 range. Print(unstable_softmax(torch.tensor()).numpy()) # prints A naive implementation would look something like this:
We want to compute the softmax over a vector of logits. This is because you not only need to make sure that all the values in the forward pass are within the valid range of your data types, but also you need to make sure of the same for the backward pass (during gradient computation). This may sound very obvious, but these kind of problems can become extremely hard to debug especially when doing gradient descent in PyTorch.

To make sure that your computations are stable, you want to avoid values with small or very large absolute value. Also, any number beyond 3.40282e+38, would be stored as inf. The smallest positive value that float32 type can represent is 1.4013e-45 and anything below that would be stored as zero. Y = np.float32(1e39) # y would be stored as inf A similar problem occurs when `y` is too large: The reason for the incorrect result is that `y` is simply too small for float32 type. Y = np.float32(1e-50) # y would be stored as zero But let's see if that's always true in practice: Mathematically, it's easy to see that `x * y / y = x` for any non zero value of `x`. You also need to make sure that the computations are stable.
#CROSS ENTROPY LOSS PYTORCH CODE#
When using any numerical computation library such as NumPy or PyTorch, it's important to note that writing mathematically correct code doesn't necessarily lead to correct results.


 0 kommentar(er)
0 kommentar(er)
